Page 20 - Impianti a fune per trasporto persone e materiali

B PROGETTAZIONE

Il coeffi ciente "c" è defi nito parametro della catenaria e, disponendo il vertice
della catenaria sull’asse verticale del sistema di riferimento, ne rappresenta l’ordi-
nata. Il suo valore è dato dal rapporto tra la tensione nel vertice della catenaria ed il
peso per unità di lunghezza della fune ("p fune ").
T T T
vertice
vertice
c = ------------------------
p fune
La componente orizzontale della tensione nella fune è sempre costante, non
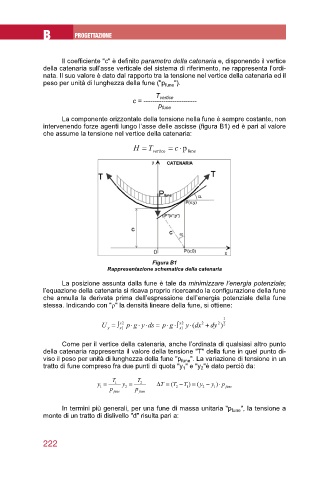
intervenendo forze agenti lungo l’asse delle ascisse (fi gura B1) ed è pari al valore
che assume la tensione nel vertice della catenaria:

H = T vertice = p ⋅ c fune

Figura B1
Rappresentazione schematica della catenaria
La posizione assunta dalla fune è tale da minimizzare l’energia potenziale;
l’equazione della catenaria si ricava proprio ricercando la confi gurazione della fune
che annulla la derivata prima dell’espressione dell’energia potenziale della fune
stessa. Indicando con "ρ" la densità lineare della fune, si ottiene:

1
⋅⋅
⋅
⋅
U =∫ x2 p gy ds = pg⋅⋅∫ x2 ydx + dy )
2
(
2 2
x1
x1
y
Come per il vertice della catenaria, anche l’ordinata di qualsiasi altro punto
della catenaria rappresenta il valore della tensione "T" della fune in quel punto di-
viso il peso per unità di lunghezza della fune "p fune ". La variazione di tensione in un
tratto di fune compreso fra due punti di quota "y " e "y "è dato perciò da:
1
2
T T
y = 1 y = 2 ∆ T = ( T − T =) ( y − y ⋅) p
1 p 2 p 2 1 2 1 fune
fune fune
In termini più generali, per una fune di massa unitaria "p fune ", la tensione a
monte di un tratto di dislivello "d" risulta pari a:
222